統計というタグが付いた記事では,自分の統計学の理解を深める,また読者の方々に統計学への興味を持ってもらうために身の回りで使われている統計モデルの紹介をしていきたいと思っています。
ブログ記事を書き溜めながら,いずれは自分の周りの出来事を統計脳で自然と考えられるようになりたいとか思っています。
今回のテーマ
皆さんは,作業に集中できないと苦しんだ経験は無いでしょうか?
その集中できないという状態を数学的に説明する研究があるそうなので,紹介したいと思います。
こちらは2014年のヒューマンインタフェース学会論文誌に掲載された京都大学の方々が書いた論文で,今回はその中で取り上げられている統計モデルを中心に紹介します。
集中力に関する研究と言いましたが,これを読むことで爆発的に集中力が継続するようになるとか魔法のようなものではありません。
作業中の「集中している」と「集中していない」状態の切り替わりはどのように起こるのかを数学的に理解しようというものです。
集中状態と非集中状態の定義
今回の研究では,簡単な計算問題や単純作業を繰り返し行い,1問にかかる時間を集中状態を表す指標と考えています。
簡単な計算問題1問にかかる時間のバラつきは集中状態の変動を表すということを仮定しています。
1問解くのにかかる時間の頻度分布を図示すると,対数正規分布に近似できる解答時間の短い山に加えて,解答時間が長い別の山が生じることが明らかになっています。
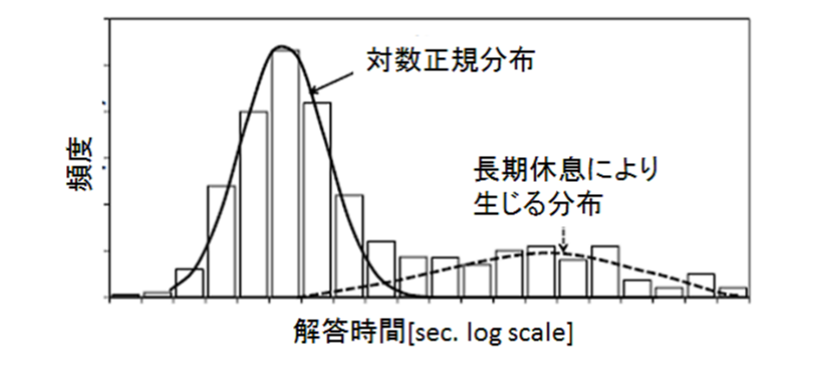
出典:知的生産性評価のための集中指標の提案 Fig.5
そこで,人間の作業中の状態を「集中状態」と「非集中状態(長期休息)」,さらに集中状態を「作業状態」と「短期休息」に分解しました。それらの状態の遷移によって,上図のような分布が生じると仮定しました。
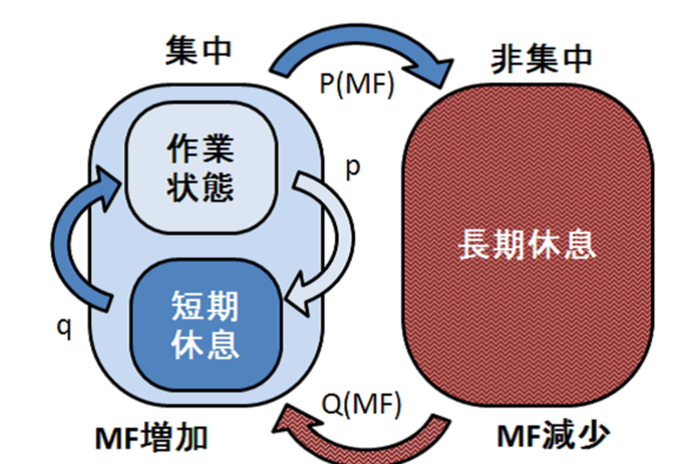
出典:断続的な休息を仮定した知的生産性変動モデルの提案 Fig.6
作業状態:作業に注力しており,作業処理が進行する状態
短期休息:作業に注力しているが,無意識に作業が中断している状態(数十ミリ秒~数百ミリ秒の休息)
長期休息:疲労などから意識的に作業が中断している状態(数秒~数十秒の休息)
図中のMFは,脳疲労値を表しており,集中状態は増加,非集中状態では減少するとしています。pとかqは確率を表しています。
集中状態における短期休息とはどういうことか?
例えば集中しているときでも,同じレベルの問題1問を解くのにかかる時間は常に同じではないですよね?
毎回微妙に違うはずです。(先ほどの頻度分布の左側の山からも分かります。)
その原因として集中状態にもレベルがあることが考えられますが,ここでは集中力は「集中」か「非集中」の2段階しかなく,集中しているときの解答時間の違いは無意識に生じる短期休息によるものと仮定しています。
f解答時間のバラつき ≒ 1問解くときに生じる短期休息の合計時間のバラつき
集中状態と非集中状態の移り替わり
集中状態から非集中状態への遷移確率は,脳疲労値を用いて以下の曲線で表現されます。
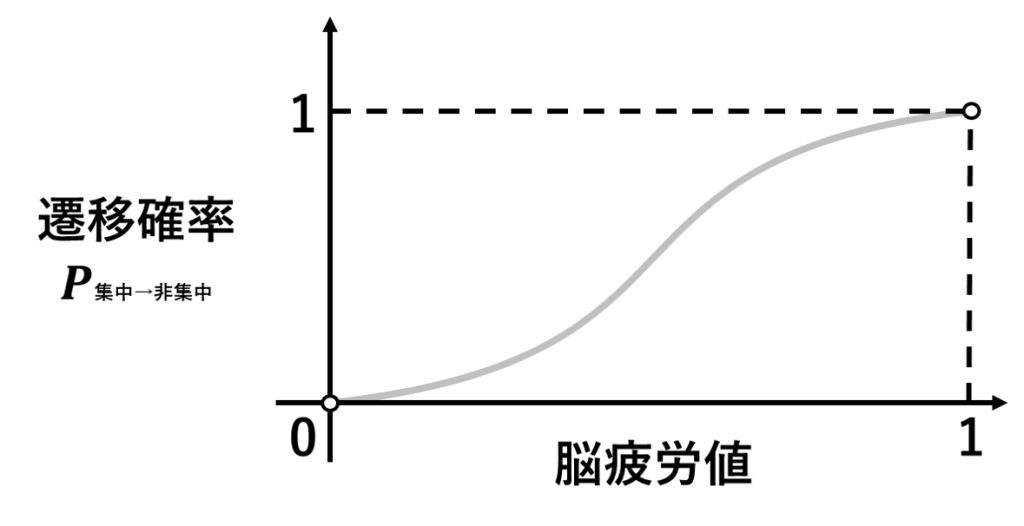
ここの詳しい解説は,ページ後半でします。
休息が大事とよく言われるのをこのモデルを用いて説明すると,脳疲労が溜まった状態で作業を続けても,非集中状態になる確率が高いので非効率ということになります。
作業が進まない状態というのは?
以上を踏まえると,作業が進まないというのは以下のどちらかが原因です。
①集中状態であっても,脳の中で短期休息の発生頻度が高い
②脳疲労が溜まっていて,非集中状態になる確率が高い
やる気で作業効率は変わるのか
今回の研究では,やる気(金銭的モチベーションの有無)で集中状態はどのように変化するのか?ということも実験しました。
実験内容の説明に関してはここでは省きますが,やる気によって短期休息の発生頻度と極端に長い長期休息の発生の減少が明らかになりました。
しかし,脳疲労の蓄積・回復速度に関しては,やる気による統計的な差は見られませんでした。
やる気があると作業効率は確かに上がるけれど,脳はやる気に関係なく疲れるみたいです。
補足
以下では論文で出てくる数理モデルの一部を紹介します。
対数正規分布
対数正規分布というものがちらっと出てきました。
短期休息の合計時間のバラつきが対数正規分布で表現されています。
なぜ対数正規分布なのか?
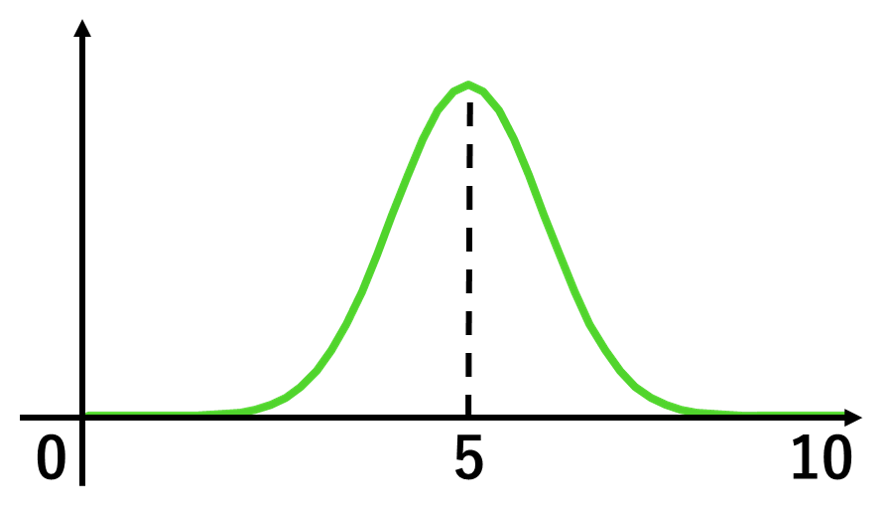
まず,正規分布とは確率分布の中で最も基礎的な分布です。
確率が中心で最も高く外にいくほど低い。理解もしやすい確率分布だと思います。
$$f(x) = \frac{1}{\sqrt{2π}σ}\exp{\left\{-\frac{(x-μ)^2}{2σ^2}\right\}}$$
期待値:μ, 標準偏差:σ
(左図:μ=5, σ=0)
ただ,時間は最小0,最大∞ですよね?
正規分布に従うと仮定すると,時間がマイナスになる可能性があります。
そのため,正規分布ではなく対数正規分布を用いて表現しています。
正規分布に比べて裾の長い確率分布です。横軸に対数を取ると正規分布になります
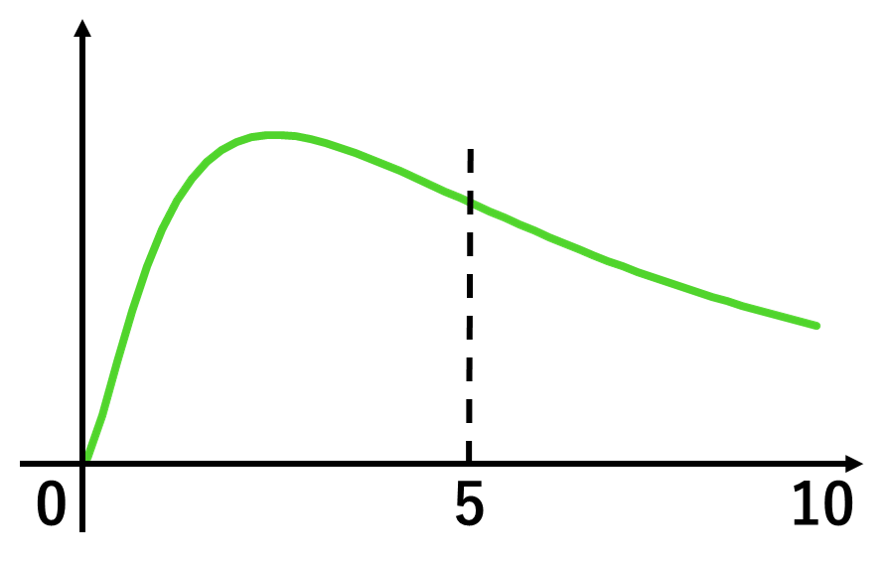
$$f(x) = \frac{1}{\sqrt{2π}σx}\exp{\left\{-\frac{(\log{x}-μ)^2}{2σ^2}\right\}}$$
左図:μ=5, σ=0
*μ, σはそれぞれ期待値,標準偏差ではないことに注意
シグモイド関数
色々な分野の数理モデルに登場する便利な関数で,ロジスティック関数とも呼ばれます。
f(x)が0~1の範囲に収まり,(0, 0.5)で点対称なので,確率f(x)で状態0から状態1に移るといった2段階の移り変わりを表現するのによく使われます。
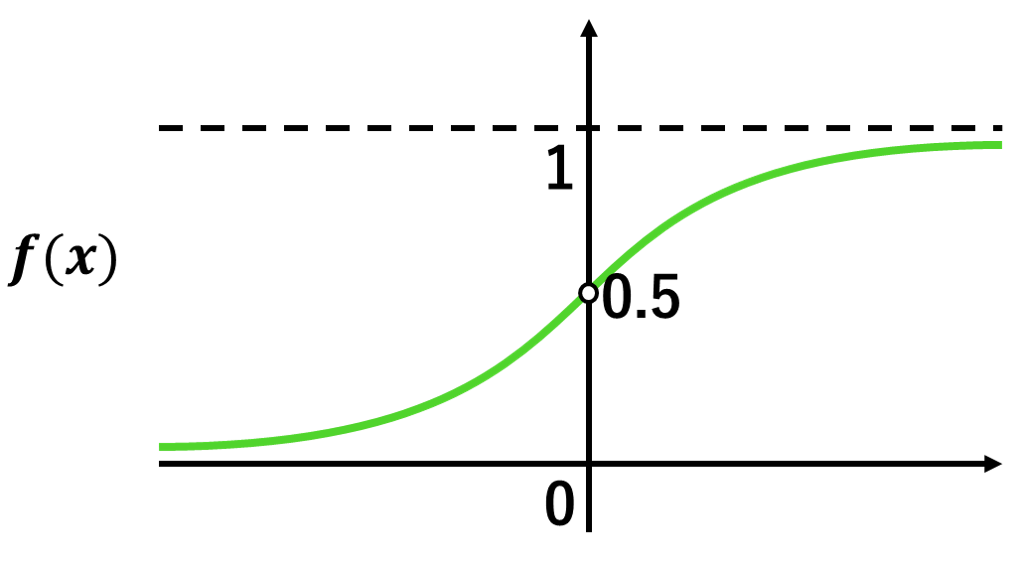
$$f(x) = \frac{1}{1+\mathrm{e}^{-αx}}$$
$$\lim_{x→-∞}f(x)=0,\ \ \ f(0)=0.5,\ \ \lim_{x→+∞}f(x)=1 $$
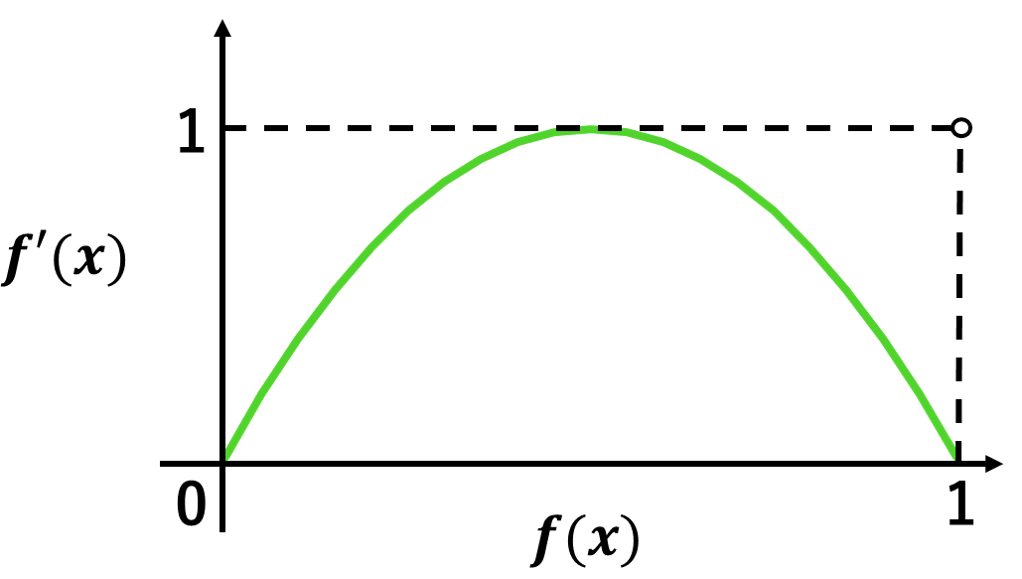
シグモイド関数は,ロジスティック方程式という微分方程式から導出することができます。
そのため,シグモイド関数は微分した方がことでモデルの解釈がしやすいと思います。
下図の最後の式がロジスティック方程式です。(厳密には,f(x)の最大値が1以外も取れるようになり,パラメータが式に加わるので微妙に変わります。)
元々は個体数の変化を表すモデルの一種で,式の解釈としては,
個体数が多いほど増加する能力も向上するけど,無限に増えることはできずある程度で限界を迎えるみたいな感じです。
\begin{eqnarray}
f'(x) &=& \frac{d}{dx} \frac{1}{1+\mathrm{e}^{-αx}}\\
\\
&=&-\frac{(1+\mathrm{e}^{-αx})’}{(1+\mathrm{e}^{-αx})^2}\\
\\
&=&-\frac{α\mathrm{e}^{-αx}}{(1+\mathrm{e}^{-αx})^2}\\
\\
&=&\frac{α}{1+\mathrm{e}^{-αx}} \left(\frac{1+\mathrm{e}^{-αx}}{1+\mathrm{e}^{-αx}}- \frac{1}{1+\mathrm{e}^{-αx}} \right)\\
\\
&=&αf(x)(1-f(x))\\
\end{eqnarray}
今回の論文では,シグモイド関数を使って集中から非集中への遷移確率を以下のように表現しています。
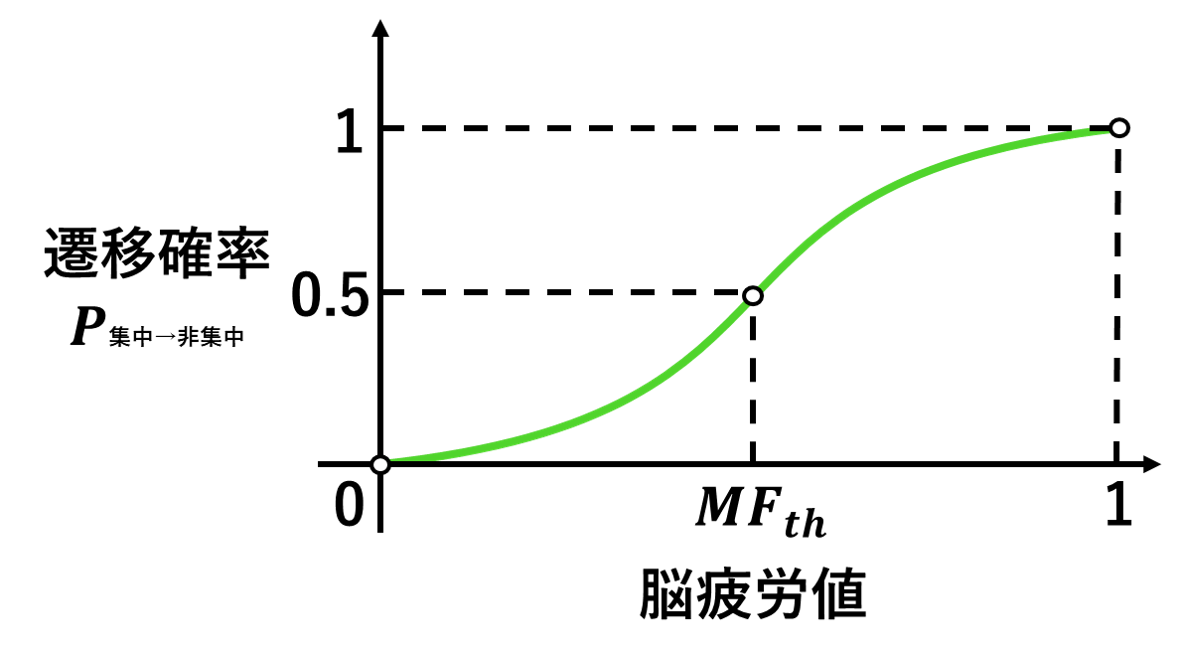
$$P_{集中→非集中}(MF) = \frac{1}{1+\mathrm{e}^{-α(MF-MF_{th})}}+c(MF)$$
MF:脳疲労値
MFth:遷移確率0.5となる脳疲労値
c(MF):P(0)=0,P(1)=1とするためのおまけ
まとめ
結局,解答時間に誤差の範囲でバラつきがあるとか,脳疲労が溜まると集中できなくなるとか当たり前のことですし,日常生活の中では役に立つことは少ないと思います。
ただ,統計モデルを用いることで,人が集中するという過程について少し分かりやすくなった気がすると思います。
こんな感じで身近なところで使われる統計モデルについての紹介をしていきたいと思っています。
以上
参考
- 断続的な休息を仮定した知的生産性変動モデルの提案
- 知的生産性評価のための集中指標の提案
- 高校数学の美しい物語 | 対数正規分布の例と平均,分散
- 高校数学の美しい物語 | シグモイド関数の意味と性質
- スマナビング!ロジスティック方程式とシグモイド関数
著者紹介



コメント